5036
1
«Как сонет Шекспира схватывает саму суть любви, или картина показывает внутреннюю красоту человека, уравнение Эйлера проникает в самые глубины существования»
Математик из Стэнфорда Кейт Девлин (Keith Devlin) написал эти слова об уравнении в эссе 2002 года, которое называлось «Самое прекрасное уравнение». Но почему от формулы Эйлера перехватывает дыхание? И что она вообще значит?
Математик из Стэнфорда Кейт Девлин (Keith Devlin) написал эти слова об уравнении в эссе 2002 года, которое называлось «Самое прекрасное уравнение». Но почему от формулы Эйлера перехватывает дыхание? И что она вообще значит?
Во-первых, буква «e» представляет собой иррациональное число (с бесконечным количеством цифр), которое начинается с 2.718281828459045… Открытое в контексте непрерывно начисляемого сложного процента, оно описывает темпы экспоненциального роста от колоний популяций насекомых до радиоактивного распада. В математике число обладает рядом неожиданных свойств, например, оно равняется сумме обратных факториалов от нуля до бесконечности. В конечном счете, константа e оккупировала математику, взявшись вроде бы ниоткуда, но оказавшись в большом числе важных уравнений.
Далее. i представляет собой так называемую мнимую единицу – квадратный корень из минус 1. «Так называемую», потому что в реальности не существует числа, которое, будучи умноженным само на себя, в результате дало отрицательное число (потому отрицательные числа не имеют действительных квадратных корней). Но в математике существует большое количество ситуаций, когда приходится извлекать квадратный корень из отрицательного числа. Число i используется как своеобразная пометка того места, где такая операция была произведена.
Пи – отношение длины окружности к ее диаметру, одна из любимых и наиболее интересных констант в математике. Подобно e, она появилась в большом количестве математических и физических формул как будто из ниоткуда.
Константа e, возведенная в степень мнимая единица, умноженная на Пи, равняется минус одному. Из уравнения Эйлера следует, что добавление к этому единицы дает ноль. Трудно поверить, что все эти странные числа, одно из которых даже не относится к реальному миру, могут быть так просто скомбинированы. Но это доказанный факт.
Далее. i представляет собой так называемую мнимую единицу – квадратный корень из минус 1. «Так называемую», потому что в реальности не существует числа, которое, будучи умноженным само на себя, в результате дало отрицательное число (потому отрицательные числа не имеют действительных квадратных корней). Но в математике существует большое количество ситуаций, когда приходится извлекать квадратный корень из отрицательного числа. Число i используется как своеобразная пометка того места, где такая операция была произведена.
Пи – отношение длины окружности к ее диаметру, одна из любимых и наиболее интересных констант в математике. Подобно e, она появилась в большом количестве математических и физических формул как будто из ниоткуда.
Константа e, возведенная в степень мнимая единица, умноженная на Пи, равняется минус одному. Из уравнения Эйлера следует, что добавление к этому единицы дает ноль. Трудно поверить, что все эти странные числа, одно из которых даже не относится к реальному миру, могут быть так просто скомбинированы. Но это доказанный факт.
Ссылки по теме:
реклама





















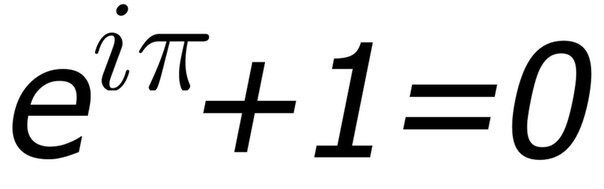
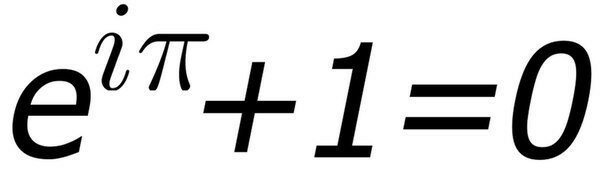














































































exp(iθ) = cosθ + isinθ
в частном случае, если θ = π, то получим:
exp(iπ) = cosπ + isinπ = -1 => exp(iπ) + 1 = 0
1) Число e (как и число 'пи') , строго говоря, 'тансцендентное' (не является корнем никакого полинома с целыми коэффициентами), т.е. еще "иррациональнее иррациональных".
2) Каноническое определение числа i sqr(i)=-1; (i в квадрате = -1)
С точки зрения домохозяек это одно и то же, но любой препод из ВУЗа скажет, что ты не прав. А про себя подумает: "ну тупой.."
3) "в реальности не существует числа, которое, будучи умноженным само на себя, в результате дало отрицательное число"
В реальности чисел вообще не существует. Никаких.
Вся математика - хитрый фундамент обозначений, аксиом, постулатов.
И уже на нем строится система интересных выводов (теоремы).
Более менее грамотно нужно было сказать, что в поле R(действительных чисел) корни из отрицательных чисел неопределены.
Но в поле C(complex) определено все. Логарифмы отрицательных аргументов, экспонента с отр. основанием, все, кроме деления на ноль. И комплексные числа НЕ БОЛЕЕ АБСТРАКТНЫ, чем действительные или даже натуральные.