2660
2
Слышали про такую? Я вот узнал уже после 30) Кстати, отличная тема для бесед, где надо произвести впечатление. =)
Я тут увлекся физикой и математикой на старости лет. Особенно прикольно читать про теорию катастроф.
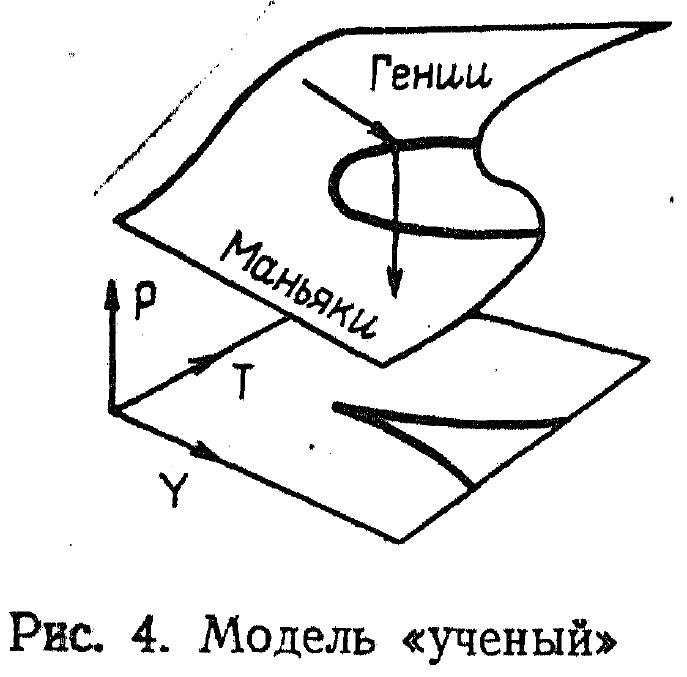
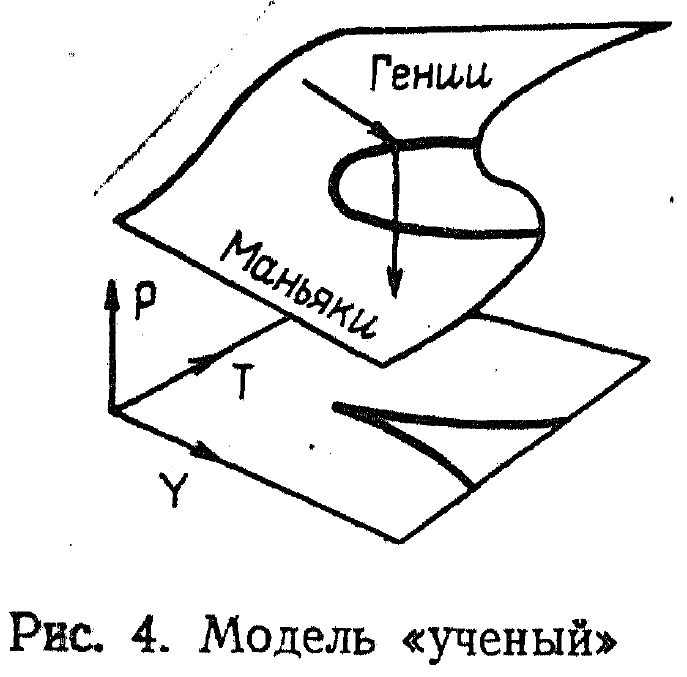
Пример принадлежит английскому математику К. Зиману и приведен в замечательной популярной книге В. Арнольда "Теория катастроф". Речь идет об описании творческого процесса ученого, и величина Д характеризует его достижения в зависимости от увлеченности (параметр У) и владения техникой и навыками исследователя (параметр Т).
Если увлеченность невелика, то достижения вяло и монотонно увеличиваются с ростом профессиональных навыков. Если же увлеченность высока, то наступают качественно новые явления: с ростом профессионализма достижения могут возрастать скачком. Такая "катастрофа" вполне желанна. Область высоких достижений в этом случае можно назвать словом "гении".
Если же рост увлеченности не подкреплен соответствующим ростом профессионализма, то происходит катастрофа в полном смысле этого слова: достижения скачком падают, и мы попадаем в область, обозначенную словом "маньяки". Интересно, что скачки из состояния "гении" в состояние "маньяки" происходят на разных линиях, и при достаточно большом значении увлеченности гений и маньяк при равной технике и увлеченности различаются лишь уровнем достижений.
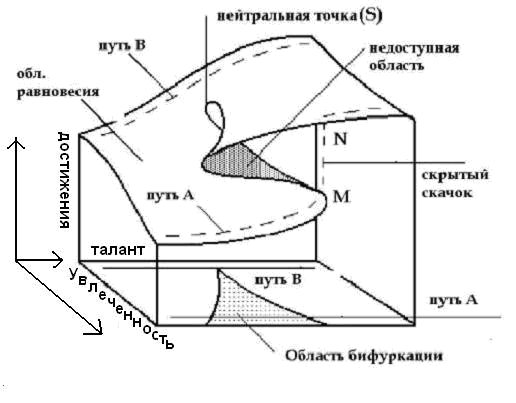
Заметим, что скачок достижений происходит при разных значениях параметров в зависимости от того, движемся ли мы слева направо или справа налево вдоль прямой A1- A2. Это так называемая петля гистерезиса, демонстрирующая, что если вы из-за потери увлеченности потерпели катастрофу в уровне достижений, то для того, чтобы вернуть их на прежний уровень, необходима значительно большая увлеченность, чем та, что имелась накануне скачка.
Несмотря на всю привлекательность и интуитивную ясность подобных рассуждений, профессиональные математики весьма скептически относятся к обоснованности построений такого рода. Однако есть и более строгие результаты, касающиеся, например, математических проблем устойчивости развивающихся во времени процессов.
Пример принадлежит английскому математику К. Зиману и приведен в замечательной популярной книге В. Арнольда "Теория катастроф". Речь идет об описании творческого процесса ученого, и величина Д характеризует его достижения в зависимости от увлеченности (параметр У) и владения техникой и навыками исследователя (параметр Т).
Если увлеченность невелика, то достижения вяло и монотонно увеличиваются с ростом профессиональных навыков. Если же увлеченность высока, то наступают качественно новые явления: с ростом профессионализма достижения могут возрастать скачком. Такая "катастрофа" вполне желанна. Область высоких достижений в этом случае можно назвать словом "гении".
Если же рост увлеченности не подкреплен соответствующим ростом профессионализма, то происходит катастрофа в полном смысле этого слова: достижения скачком падают, и мы попадаем в область, обозначенную словом "маньяки". Интересно, что скачки из состояния "гении" в состояние "маньяки" происходят на разных линиях, и при достаточно большом значении увлеченности гений и маньяк при равной технике и увлеченности различаются лишь уровнем достижений.
Заметим, что скачок достижений происходит при разных значениях параметров в зависимости от того, движемся ли мы слева направо или справа налево вдоль прямой A1- A2. Это так называемая петля гистерезиса, демонстрирующая, что если вы из-за потери увлеченности потерпели катастрофу в уровне достижений, то для того, чтобы вернуть их на прежний уровень, необходима значительно большая увлеченность, чем та, что имелась накануне скачка.
Несмотря на всю привлекательность и интуитивную ясность подобных рассуждений, профессиональные математики весьма скептически относятся к обоснованности построений такого рода. Однако есть и более строгие результаты, касающиеся, например, математических проблем устойчивости развивающихся во времени процессов.
Ссылки по теме:
- Большой переезд: куда могут переселиться земляне?
- Стивен Хокинг перед смертью рассказал, чего боялся больше всего
- Дедуля разнес отделение Cбербанка из-за "шайтан-машины"
- 15 бесплатных обучающих курсов - без СМС и регистрации
- Божественный полет семени