18927
7
Интересные факты, которые по настоящему не смогут оценить лишь гуманитарии. Кто бы знал, что кому-то вздумается округлять число Пи...
1.
2.
×
3.
4.
5.
6.
7.
Источник:
Ссылки по теме:
- В копилку эрудита: интересные факты о бизнесменах
- 30 фактов об океане, от которых у вас захватит дух
- Самые странные факты об Альберте Эйнштейне
- 10 по-настоящему интересных фактов, которые вы могли не знать
- Вы могли этого не знать: 15 интересных фактов о сериалах
реклама




















































































Не зря на некоторых сайтах любят перечслять разных знаменитостей, родившихся именно в данный текущий день. Т.е. вероятность совпадения гораздо ниже, чем тут заявлено.
Математики, похоже, имели в виду лишь совпадающее число месяца, но журналисты, как всегда, все переврали.
https://ru.wikipedia.org/wiki/Парадокс_дней_рожденияhttps://ru.wikipedia.org/wiki/Парадокс_дней_рождения
А вот с месяцами уже сложнее.Хотя можно подобрать первую группу зимних и осенних а вторую весенних и летних.Уже не будет совпадения.Только внутри группы.
И да, я не одинок в этом.
У нас на работе тоже коллектив не маленький и у нас точно есть пары 2-3, у которых ДР выпадает на одну дату.
например в вашем примере с группой из 250 человек будет более 31 000 вариантов пар. что, учитывая 365 дней в году дает более чем неплохие шансы на совпадение даты рождения. да 100% даёт только группа из 367 человек, но смысл в том что в группе из 57 человек шанс этого 99% и с увеличением числа людей просто прибавляется число 9 после запятой т.е. 99.9...9%
Вопрос - не в точности проведенных математических расчетов, а в правильной интерпретации их результатов.
Математически доказанное утверждение о том, что в группе от 23 человек и выше с вероятностью .... процентов найдется хотя бы одна пара с совпадающими днями рождения НЕ означает, в общем случае, что В ЛЮБОЙ группе от 23 человек ОБЯЗАТЕЛЬНО найдется такая пара (и тем более, несколько пар).
Именно потому, что данное утверждение - вероятностное.
И, в общем случае, ЛЮБАЯ рассматриваемая группа численностью от 23 человек может оказаться принадлежащей как раз к той, оставшейся доле вероятности. С несовпадающими днями рождения.
И я даже не говорю о том, что и сама референсная группа из 23 человек может изначально быть сформирована по принципу несовпадения дней рождения.
Ну вот захотелось так, например, учителям в школе при формировании списков учеников класса. Нет оснований утверждать, что такое невозможно, ибо не запрещено, хотя по факту вряд ли кто станет так специально заморачиваться.
Кстати, школьные классы - прекрасный пример. В советское время, например, в свой день рождения КАЖДЫЙ ученик класса угощал одноклассников конфетами. По крайней мере, в моей школе так было принято.
И вот, представьте себе, ни одной пары учеников с совпадающими днями рождения в моих школьных классах НЕ было.
Это - сермяжная правда, а не абстрактные, хотя для кого-то и занятные математические выводы.
в моём классе совпадали даты рождений у двух пар))
" - 50%"
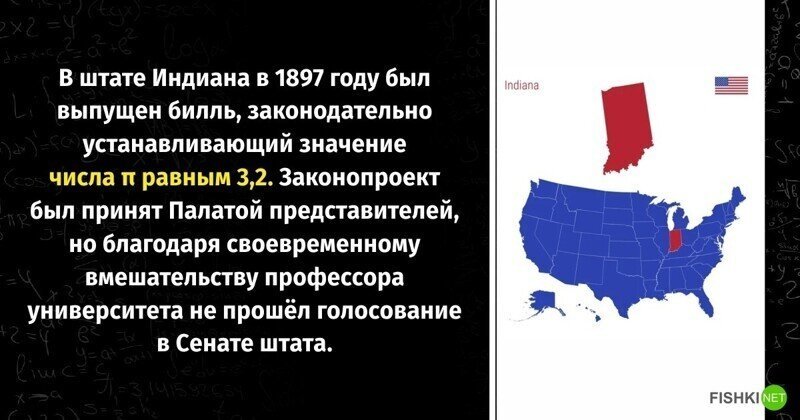
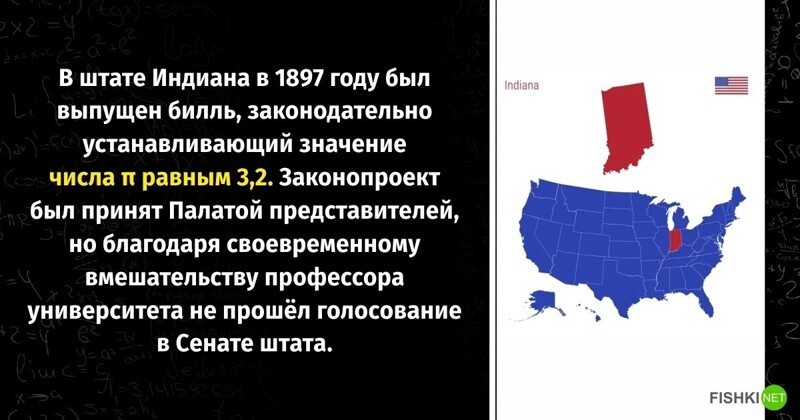
Там просто один гражданин решил, что он решил квадратуру круга (утопия, задача нерешаемая в принципе) и захотел это увековечить.
Хотя скорее себя))
Ну в парламенте всё-таки не математики сидят, поэтому с начала у него получалось.
Но когда об этом стало известно людям, его быстро "успокоили".
https:https://ru.m.wikipedia.org/wiki/Законопроект_о_числе_пиhttps://ru.m.wikipedia.org/wiki/Законопроект_о_числе_пи
g = 10
e = 3
50%, либо встретите. либо нет...
========
у нас в конторе 120 человек - совпадения с моим ДР нет
С точки зрения тер.вера это доказывается неоспоримо, но вот на первый взгляд выглядит весьма сомнительно
Дети! Сколько будет пятьи пять?
Учител! пятипять приблызительно будет двацатри двацачетыри.
Дети! Я сколко раз вам буду гаварить, что пятипять приблызительно будет двацашесть двацасем!
Учитывая что среди простых чисел всего одно четное - это два, а сумма 4-х нечетных чисел всегда четное число, то сумма четырех простых чисел может быть (но не обязано) быть простым, только если оно содержит 2
Так как двойка самое меньшее простое число, то такая последовательность единственная 2 3 5 7. Сумма этих чисел чисто случайно оказалась простым числом
Кстати сумма двух простых чисел 2 и 3 тоже дает 5 - просто число
Сумма 6 простых чисел 2 3 5 7 11 13 = 41, тоже простое
А вот сумма никакой последовательности идущих подряд 8 простых чисел простым уже не является.
На самом деле таких фактов я думаю можно накопать достаточно много.
Кстати, если речь пойдет о последовательности нечетной длины, то там уже все гораздо сложнее
Вот чисто пример: зачем во многих языках программирования, или даже в Экселе, есть просто функция округления, есть функция округления в большую сторону, есть в меньшую сторону. Это различные варианты округления. И если эти функции есть, то кому-то то они нужны. Разве нет?
А учился я достаточно, в советской школе и там нам не рассказывали об округлении в меньшую сторону, видимо это очень специфичное правило. В институте, в НИГАИКе, тоже об этом не упоминали и, геодезируя, я округляю по стандартному правилу.
Функция «адвоката дьявола» заключалась в том, чтобы собрать и привести все возможные аргументы, которые могли бы помешать канонизации или беатификации праведника. Официальное лицо, выполнявшее противоположную функцию (то есть защиту претендента), называлось «защитник Бога» (лат. advocatus Dei). До 1983 года ни один акт канонизации или беатификации не мог быть признан законным, если при этом акте не присутствовал «адвокат дьявола».
и при чем тут американцы?
Ф -фантазер